1.概述
在 35C3 wallet.fail 的渗透测试中,我们(Thomas Roth, Josh Datko, Dmitry Nedospasov)发现了硬件钱包不少的漏洞。其中之一是,Ledger Blue 加密货币钱包的 RF 侧信道攻击漏洞:如下视频所示,在钱包上输入 PIN 码时,每输入一位便会产生一个频率在 169 MHz 左右的电磁波谱。我们的想法是,用 TensorFlow 机器学习自动化分析这些信号,并恢复(提取)PIN 码。

用来搜索和接收这样一个信号的设备,从极其简陋的,到极其复杂精密的都有,尽管其核心都是 SDR(Software Defined Radio, 软件定义无线电)。一套廉价的 RTL-SDR 接收器大约为 30 美刀,而更加复杂的设备如 HackRF 或 bladeRF 可提供更高的取样频率以及更高的 ADC 分辨率。例如,上述视频中展示的设备是 HackRF 带一根可伸缩天线:

尽管如此廉价的设备,依然可以接收 2 米之外的信号。如果使用定向天线的话,这个距离还可以更远。另外,我们还发现,连接到设备的 USB 线缆使得接收到信号的强度显著增强。
接下来的问题是:是硬件钱包的哪条总线泄露出的信号 ? 将接收到的信号图形化,可以看到 11 段脉冲,1 段 0 电平,接下来又是脉冲。
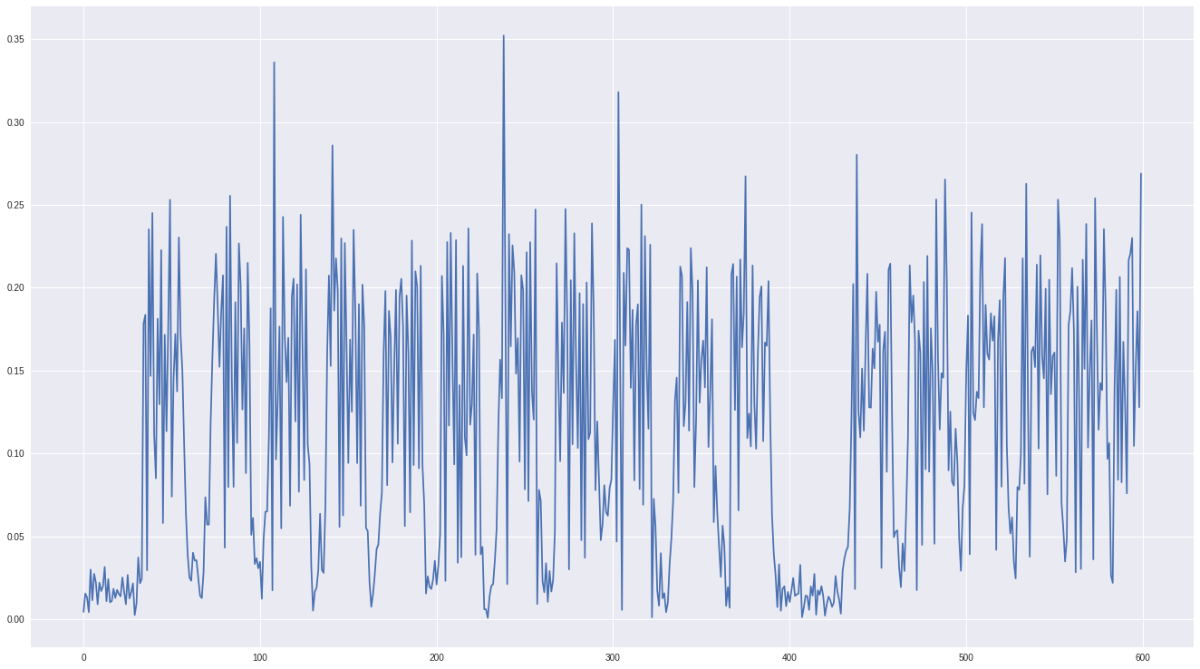
利用逻辑分析仪,我们确认这些信号送往屏幕的。开头的 11 字节包含的是(数字按键的)位置信息(X、Y 坐标,宽度和高度),其后是数据信息。如果你仔细观看过上面的视频,会发现显示屏上每一位数字按下时,都会以蓝色的背景重新刷新屏幕。由于屏幕键盘上不同的数字按键有不同的 X、Y 坐标,所以仅凭信号波形前面的 11 字节,就足以恢复 PIN 码。也就是说,现在我们的目标是构建一个神经网络——能通过接收到的无线信号,获得输入的 PIN 码。
2.收集训练数据
为了训练神经网络,必须要有大量的训练数据。在当前条件下,就是许多带标记的按键信号。例如,数字 0 的 100 次点击信号数据,数字 1 的 100 次点击信号数据,等等。由于数据采集工作量巨大,我们决定采用自动化的方法处理。我们用 Arduino,伺服电机和其他一些器件,组装了一台“按键点击器”。如下图:

结合 GNU Radio 以及精确地控制,我们有了收集神经网络训练数据的完美工具。GNU Radio 非常简单,由 Osmocom 源和文件接收器组成,如下图所示,只不过实际的控制更为精密:
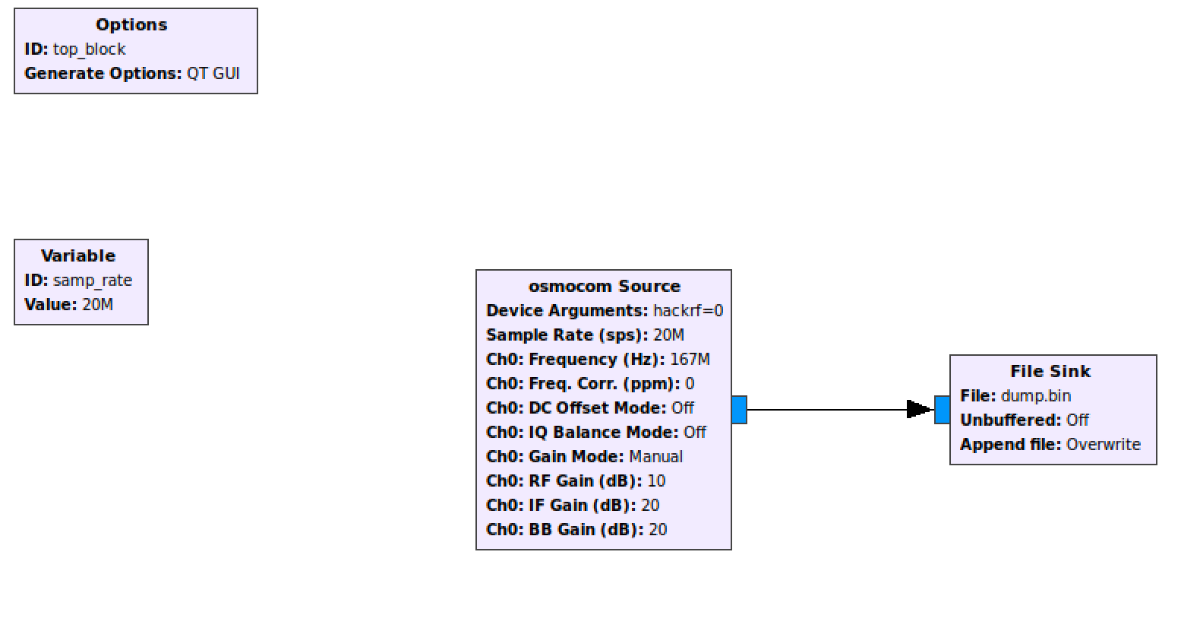
为了让这套装置在家里能使用,我们近距离采集了训练数据集(数字 7,8,9,0 的 50 份样本)。当然,采集更多的训练样本效果更好。不过,正如我们文章展示的,尽管如此少量的数据,我们依然可以得到一个工作得非常好的神经网络。
3.准备 TensorFlow 的数据
本案例完整的 Jupyter Notebook 包括所有的数据源和步骤,都上传到网上了!大家可以自由下载使用。
下载和解压数据之后,我们可以绘制出这些样本数据,确保数据确实就是我们需要的。现在我们绘制出这些 I/Q 信号的实部以及绝对值。我们可以清楚地看到这 11 个字节:
|
1
2
3
4
5
|
data0 = np.load("try_0_1_short.npy")[:data_length]
plt.figure()
plt.plot(data0.real)
plt.plot(np.abs(data0))
plt.show()
|
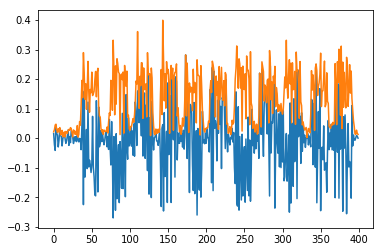
按照这种方式,如果我们绘制两个不同的数字(例如,数字 0 和数字 7 ),可以看到信号波形并没有明显的差异:
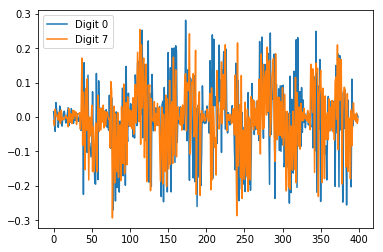
如果我们给它加一个简单的带通滤波器,信号之间的差异瞬间就很明显:
|
1
2
3
4
5
6
7
8
9
10
11
|
bandpass_start = 0.55
bandpass_end = 0.60
bandpass_order = 4
def apply_bandpass(s, order=bandpass_order, low=bandpass_start, high=bandpass_end):
b, a = signal.butter(order, [low, high], btype='band')
zi = signal.lfilter_zi(b, a)
z, _ = signal.lfilter(b, a, s, zi=zi*s[0])
return z
|
用经过滤波后的数据再次进行绘制,我们可以看到两个数字信号之间有明显的差别:
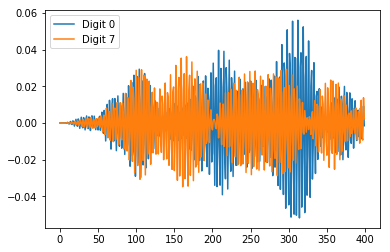
带通滤波器不仅能滤除噪声,还能平滑不同数字波形之间的差异(对比上述两幅图片易得)。通过对信号进行滤波处理,使得我们神经网络的训练工作减轻了许多:由于不同数字的信号更容易区分,我们仅用更少的数据还能得到更好的结果!
4.加载,标记,分组
现在,我们知道我们得先对数据进行预处理,是时候开始动手了。有一点需要注意的是,在训练一个神经网络时,最开始就把所有的数据分为两组是很重要的:
- 训练数据集:用于训练神经网络。
- 测试数据集:用于在所有的训练完成、神经网络参数确定后,验证神经网络的可靠性。
绝不能把测试数据既用来训练神经网络,又用来测试网络,这是很重要的原则。否则的话,会导致网络针对测试数据过度优化,而不是正常的无偏向网络。在我们的案例中,每位数字有 50 条数据,所以我们用其中的 40 条来训练,剩余的 10 条用于测试。
我们的数据处理流程是这样:
- 分别从各个样本文件加载 40 个 I/Q 样本
- 带通滤波处理
- 取滤波后信号的绝对值
- 把数据转换成 20x20 的矩阵(便于后面的可视化处理)
- 用 MinMaxScaler 归一化到 0.0 与 1.0 之间
- 把数据、数据的标记(本案例中即信号代表的按键数字)放入两个数组中
- 打乱每对数据(数据本身+数据标记)在两个数组内的顺序
该部分的详细代码见 Jupyter Notebook
如果现在把数据绘制成图形,可得到下图所示的二维图形:数据已经归一化到了 [0.0,1.0] ,带通滤波效果良好。
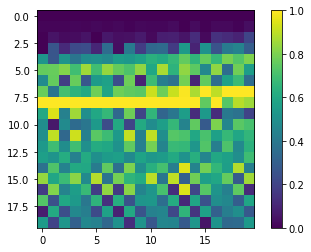
5.构建神经网络
我们用到的网络与 TensorFlow 官方教程中的非常相似,如果你有兴趣想详细了解这方面的内容,不妨多打开 Jupyter Notebook 中的参考链接。
我们的神经网络有 3 层:
- Flatten layer:把平面的二维数组转换成一维
- Dense layer:128 路输出的层,使用 Rectified Linear Unit(ReLU)激活函数
- Dense layer:10 路输出的层(1 位数字 1 路输出),使用 SoftMax 激活函数
我们神经网络的核心代码如下:
|
1
2
3
4
5
|
model = keras.Sequential([
keras.layers.Flatten(input_shape=(20, 20)),
keras.layers.Dense(128, activation=tf.nn.relu),
keras.layers.Dense(10, activation=tf.nn.softmax)
])
|
以上便是整个的流程!请自行随意调试,比如在中间增加网络层数、改变输出路数等等。
接下来,编译我们的神经网络。为此,我们需要指定优化器。AdamOptimizer 是个很棒的通用优化器。我们还需要指定误差函数以及确定一个度量值来衡量我们网络是性能。在当前案例中,我们所关注的度量值是准确度(即神经网络区分数字信号的准确程度)。
|
1
2
3
|
model.compile(optimizer=tf.train.AdamOptimizer(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
|
6.训练神经网络
现在,我们已经定义好了网络,编译好了模型,可以开始训练神经网络了。这个过程只是简单的调用 fit 函数以及训练数据和数据标记 。我们还指定了网络训练的次数(使用 epoch 参数),以及如何把数据分为训练数据和验证数据:
|
1
|
history = model.fit(train_data, train_labels, epochs=200, verbose=0, validation_split=0.2)
|
根据训练数据的多少以及 epochs(轮次) ,这个过程花费的时间不定。我们把训练的结果绘制成图形,来分析 epochs(轮次) 是如何影响我们的误差(Loss,与正确结果的偏离程度)和 准确度(Accuracy ):
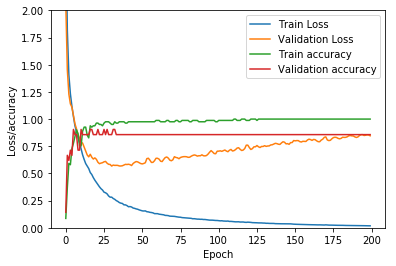
不可思议的事情发生了:我们训练神经网络的轮次越多,验证时误差也越高!
这是在机器学习中非常常见的过拟合现象:神经网络被同一组数据训练的次数过多,网络学会了精确区分训练集,而不是学习不同训练信号的差异!对此,我们需要在准确度与误差之间找到一个平衡点,从图上来看,这个位置介于 28 到 50 之间。
举个例,如果我们训练神经网络的 epoch 为 30 ,则我们得到的误差将会低于 200 epoch 时:
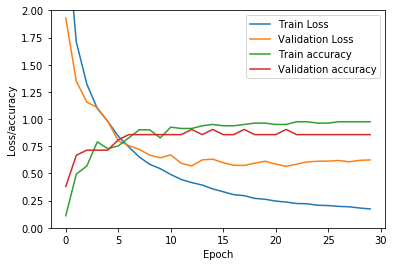
好了,现在我们已经有了一个完全训练好的神经网络!我们来测试它的效果。
7.测试神经网络
检验真理的时刻到了:对这些陌生的数据,神经网络表现如何呢 ?还记得我们的测试数据是最初的时候分组分出来的吧 ?我们将用这些数据来测试神经网络的准确性!
|
1
2
|
test_loss, test_acc = model.evaluate(test_data, test_labels)
print('Accuracy on testdata:', test_acc * 100, "%")
|
|
1
2
|
26/26 [==============================] - 0s 58us/sample - loss: 0.1962 - acc: 0.9615
Accuracy on testdata: 96.15384340286255 %
|
哇!96% 的准确率!我们的神经网络表现非常不错。我们可以通过绘制出输出层的结果,可视化神经网络的性能,看看网络对每个结果的准确度:
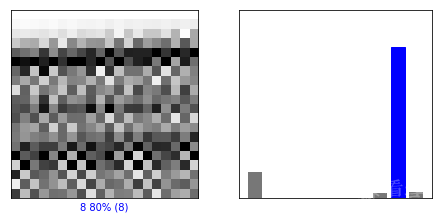
上图左侧是数据本身,图片下方的标记表明神经网络判定这个信号 80% 的可能性是数字 8 。右侧,我们可以看到不同数字的权重:数字 0 在最左边,数字 7,8 和数字 9 在右边。数字 8 是妥妥的赢家!
我们可以把整个测试数据集的结果绘制出来,由图可以看到只有 1 次判断错误!

8.总结
我希望这篇短文可以让你洞察如何用机器学习自动化地分析电磁波侧信道数据。当然,机器学习的能力并不仅限于 RF 侧信道。对于如电源 SCA trace,time SCA trace 等的分析同样适用。
如果对学习包括侧信道攻击在内的更多 IoT 及硬件安全内容感兴趣,不妨来我们的 IoT&hardware security 训练营。我们也提供嵌入式安全的全领域咨询服务,随时联系!
原文:https://leveldown.de/blog/tensorflow-sidechannel-analysis/
2020安全开发者峰会(2020 SDC)议题征集 中国.北京 7月!
转载自看雪
最后于 2020-3-26
被aiyun编辑
,原因: